|
|
Truss is a structure comprising straight members forming one
or more triangular units. The members of the truss are connected at
the ends usually by pin-joints. The joint of a truss are commonly
known as nodes. External forces and reactions are considered to act
only at the nodes and result in forces in the members which are only
axial forces (tensile or compressive).
When all the members and nodes lie within a two dimensional
plane, it is known as plane truss, whereas a truss having members
and nodes extending into three dimensions is known as space truss.
Trusses are used in many
structures
like bridges, roof supports,
transmission towers, space stations etc. Different types of simple plane truss like
Warren truss, Pratt truss, Howe truss, roof truss etc are shown in
figure 2-1
Truss can be termed as;
(a) statically determinate;
all the unknown forces (support reaction and member forces)
can be determined by applying equations of
static equilibrium. if m+r = 2j,
(b) indeterminate;
equations of static equilibrium are not sufficient to determine
unknown forces, if m+r > 2j,
(c) unstable;
not suitable to carry load; if m+r < 2j;
Where m= number of members in a truss;
r = number of reaction components;
j= number of joints in a truss;
|
Featured Links
Moment of Inertia
calculatorNew
For different sections including I-section and
T-section.
Deflection
Calculator
Easy to use calculator for different loads on beams
Problem SolverNew
A collection of illustrated solved examples for civil
engineers.
RC Beam CalculatorNew
Calculate the strength of reinforced concrete beams
Reinforced
concreteNew
Analysis and design of reinforced concrete structures
Bending Moment
calculatorNew
Calculate Bending moments for simply supported beams
CE QUIZNew
A collection of quiz in different areas of civil
engineering
CE HorizonNew
Online Civil Engineering Journal and Magazine |
|
Methods of Analysis There are two methods for solving for
the forces in the members of a truss;
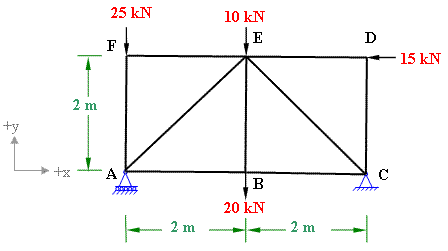
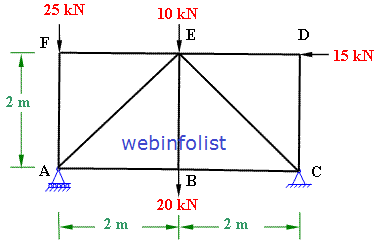
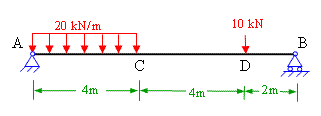
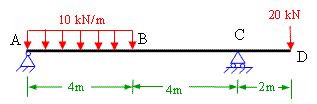
(i) Method of Joints: In this methods we consider the
equilibrium of the all the joints of the truss. Only two equations of
static equilibrium, Σ Fx and Σ Fy.
Therefore it is very important in this method that we should start
with the joint having not more than 2 unknown forces. see
problem 3-1
(ii) Method of sections: This method is used when the
forces in a few members are to be determined. In this method an
imaginary section is passed through the members in which the force
is to be determined and then consider the equilibrium of the left
hand side or the right hand side of the truss to find unknown forces. see
problem 3-2
For solved problems please visit our
Problem SolverNew
|
|
Profile of Civil EngineersNew
Get to know about distinguished civil engineers
|
