Procedure for Developing Influence Line Diagram

Influence line diagram (ILD) can be developed by the following ways;

(a)   by independently applying a unit load at several positions on the structure and determining the structural response (reaction, shear, moment etc.) by applying the principles of statics. Tabulate these values and then plot the graph of load position(along x-axis)  vs the structural response (along y-axis). You can also use online calculator to get the ordinates of ILD.

(b)   write the equation for structural response due to a unit load at a distance 'x' by applying the principles of statics. This will give the equation of influence line in terms of 'x' for different parts of the span.

(c)   Muller-Breslau Principle which gives qualitative influence lines. This principle states that the influence line for a function is to the same scale as the deflected shape of the beam when the beam is acted upon by that function. By using these techniques we can quickly draw the shape of an influence line.

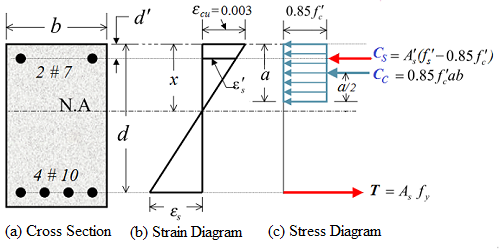
To explain the procedure of developing influence line we consider a  beam of span L and apply a unit load at a distance x from the support A as shown in figure 1.

Influence line for Reaction at a support

Calculating the reaction at supports we get;

R_B = x/L   (straight line equation)

R_A = 1- x/L   (straight line equation)

The influence line diagrams for R_B is plotted in figure 1(a) which shows that the value of R_B is x/L when the unit load is at a distance x from A and it would be equal to 1 when the unit load will be at B.

Similarly the ILD for R_A  plotted in figure 1 (b) shows that the value of R_A   will be 1 when unit load is at A and it would be equal to 1-x/L when the unit load is at a distance x from support A.

Influence line for Shear Force at a section

F_C = -R_B = - x/L  ;when load is between A and C

F_C = R_A = 1- x/L   ;when the load is between C and B

The ILD for F_C plotted in figure 1(c) clearly indicates the above values. Maximum positive or negative shear force will occur at C when the load is placed at C.

Influence line for Bending Moment at a section

M_C = R_B . (L-a)    ; when unit load is between A and C.

       = x (L - a )/L = x (1-a/L)

M_C = R_A .(a)    ; when unit load is between C and B.

      = (1 - x/L)(a)

When unit load is at C the bending moment at C would be maximum as can be seen below;

M_C = a (L - a) / L              ;when unit load is at C.

The ILD for M_C  plotted in figure 1(d) clearly indicates these values.

It is evident from the above equations and their plot that influence line diagram is a straight line in all the cases.

Please watch our following video lectures about moving load analysis

Video Lecture on Analysis of Moving Loads
This video lecture is about developing influence line diagram for shear force and bending moment to do analysis of structures in case of moving loads.

Video Lecture on Maximum Shear Force at a section due to a series of moving loads
This video lecture explains the trial and error procedure for determining the value of maximum shear force at a section due to a series of moving loads. It includes a solved example also.

Video Lecture on Maximum Bending Moment at a given section due to a series of moving loads
This video lecture is about determining maximum bending moment at a given section and the absolute maximum bending moment due to a series of moving loads on a simple beam

Applications of Influence Line Diagram

You can also use the following calculators for Moving Load Analysis

Calculator for Moving Load Analysis for Maximum B.M. at a section of simple beam

Calculator for Absolute Maximum B.M. due to moving loads for simple beam