Applications of Influence Line Diagram

Applications of Influence Line Diagram

From the influence line we can determine the response (reaction, shear, moment etc.) of a structure due to multiple point loads as well as due to uniform load. Influence line also helps in finding the maximum value of a response function.

Response due to Point Load

Response due to single point load = magnitude of load x ordinate of ILD at the position of point load.
Response due to multiple point loads = equal to the algebraic sum of the product of load and the corresponding ordinate of ILD.

Please watch our following video lectures about moving load analysis

Video Lecture on Analysis of Moving Loads
This video lecture is about developing influence line diagram for shear force and bending moment to do analysis of structures in case of moving loads.

Video Lecture on Maximum Shear Force at a section due to a series of moving loads
This video lecture explains the trial and error procedure for determining the value of maximum shear force at a section due to a series of moving loads. It includes a solved example also.

Video Lecture on Maximum Bending Moment at a given section due to a series of moving loads
This video lecture is about determining maximum bending moment at a given section and the absolute maximum bending moment due to a series of moving loads on a simple beam

Illustrative Example: Consider A simply supported beam (figure 1) having a span of 7 m.

The reaction at support B due to 10 kN load will be equal to (10) x (value of ordinate at 2m from the ILD for R_B) = 10 x (2/7) = 20/7 kN.

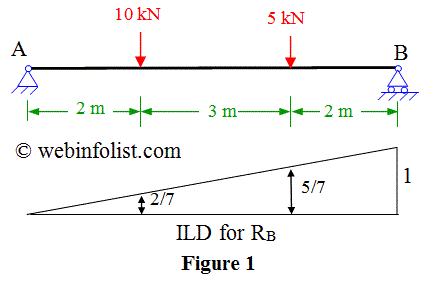
Similarly the reaction at B due to 5 kN load would be equal to (5) x (value of ordinate at 5 m from the ILD for R_B) = 5 x (5/7) = 25/7 kN
Reaction at support B due to both the loads = 10 x (2/7) + 5 x (5/7)
                           = 20/7 + 25/7 = 45/7 kN = 6.43 kN

Response due to Uniform Load

Response due to uniform load is equal to the intensity of load multiplied by the area of ILD under the load.

Consider a beam of span 5m shown in figure 2 and loaded with a 3 m long uniform load of intensity 7 kN/m as shown.

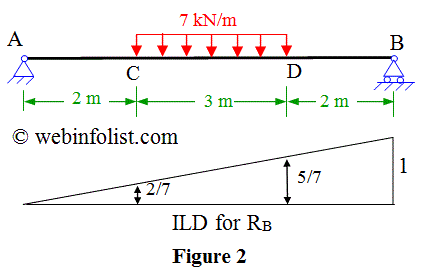
The value of reaction at B due to this uniform load =

 (intensity of uniform load) x (area of ILD between C and D).

area of ILD between C and D = area of trapezium

=0.5(ordinate at C+ordinate at D) x (length of uniform load)

                      = 0.5 (2/7 + 5/7) (3) = 0.5 (7/7) (3) = 1.5

therefore, Reaction at B = (7) (1.5) = 10.5 kN

You can also use the following calculators for Moving Load Analysis

Calculator for Moving Load Analysis for Maximum B.M. at a section of simple beam

Calculator for Absolute Maximum B.M. due to moving loads for simple beam