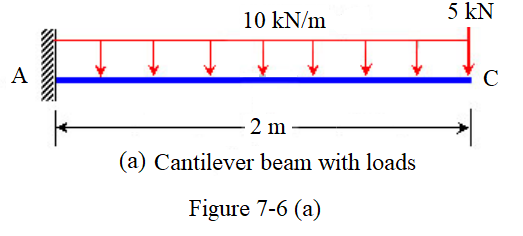
Use moment-area theorems to determine the slope and deflection at free end of the cantilever beam given above in Figure 7-6(a)
Please click here to to get the complete solution of this problem
You can also solve this problem by using online calculator for slope and deflection.
Leave a Reply
You must be logged in to post a comment.