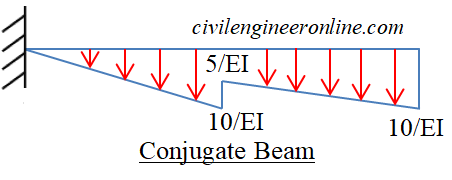
Conjugate beam is an imaginary beam which is helpful to determine the slope and deflection of a beam.
Get more information about Conjugate beam and its application to solve for slope and deflection in the following link

Conjugate beam is an imaginary beam which is helpful to determine the slope and deflection of a beam.
Get more information about Conjugate beam and its application to solve for slope and deflection in the following link
Copyright © 2025 | WordPress Theme by MH Themes
Leave a Reply
You must be logged in to post a comment.