Problem 5-6

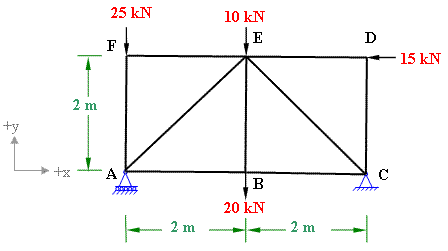
Determine the values and draw the diagrams for shear force, bending moment and axial force due to the imposed load on the frame shown in figure 5-6(a). Support at A is hinged and F is roller. Joints at C and E are rigid joints.

Figure 5-6(a)

Solution:

The support A is hinged, it will have two reactions (horizontal H_A and vertical V_A). Support F is roller, it will have only vertical reaction V_F. To calculate the support reactions we apply equilibrium equations.

Assuming horizontal reaction (H_A) at A in the left hand direction and apply equilibrium of the frame in horizontal direction, we get;

Σ H = 0; ---- (Eq. 1)

- H_A + 5 = 0 ;

Therefore reaction H_A = 5 kN in the left hand direction.

Consider equilibrium of frame in vertical direction, we get;

Σ V = 0;

V_A + V_F - 10 x 2 = 0;

V_A + V_F - 20 = 0; ---- (Eq. 2)

Consider rotational equilibrium of frame and taking moment of all the forces about point A, we get;

Σ M_A = 0;

V_F x 5 - 10 x 2 x 1 - 5 x 3 = 0; (considering clockwise moment as negative and anti-clockwise moment as positive)

5 V_F - 20 - 15 = 0; ---- (Eq. 3)

We get, V_F = 7 kN

Now we substitute this value of V_F in Eq. 2 to get the value of V_A;

V_A + 7 - 20 = 0; therefore V_A = 13 kN. Negative sign indicates that the reaction at A will be in the downward direction as shown in the free body diagram of the frame.

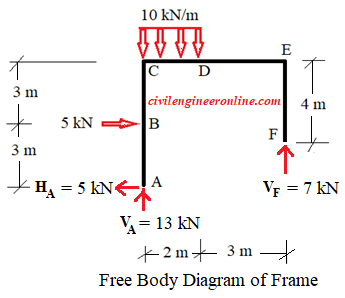
Figure 5-6(b)

Now we draw the free body diagram of each member ABC, CDE and EF as well as the free body diagram of rigid joints C and E and apply the equilibrium equations.

Figure 5-6(c)

Equilibrium of vertical member ABC:

We cut a section just before rigid joint C. This will give three unknowns at the section V_C, H_C, and M_C.

Consider horizontal direction as x-axis and vertical as y-axis.

Apply equilibrium in horizontal direction.

Σ F_x = 0; - 5 + 5 - H_C = 0. This gives H_C = 0.

Apply equilibrium in vertical direction.

Σ F_y = 0; 13 - V_C = 0. This gives V_C = 13 kN

Apply moment equilibrium by taking moment of all the forces at A. Considering clockwise moment as negative and anticlockwise as positive, we get;

Σ M_A = 0.

- 5 x 6 + 5 x 3 + M_C = 0.

This yields M_C = 15 kNm as shown in figure.

Now consider the equilibrium of rigid joint C. These calculated values of H_C, V_C and M_C will be now applied in equal and opposite direction at C. There is no horizontal force at C. The rigid joint C will transfer these values of V_C and M_C to the other member CDE as shown in figure 5-6(c).

Equilibrium of horizontal member CDE:

There is no horizontal force acting on CDE. We consider wquilibrium in horizontal direction.

We apply Σ F_y = 0; 13 - 10 x 2 + V_E = 0.

This gives V_E = 7 kN.

Apply Σ M_C = 0. We get - 15 - 13 x 5 + 10 x 2 x 4 + M_E = 0. Therefore M_E = 0.

Now apply equal and opposite value of V_E on the other side of the section at E on the rigid joint E and transfer this force to member EF on the other side of the joint.

We consider the quilibrium of vertical member EF and confirm that Σ F_Y = 0; This shows that our calculations are correct. The updated Fee body diagram is shown in Figure 5-6(d)

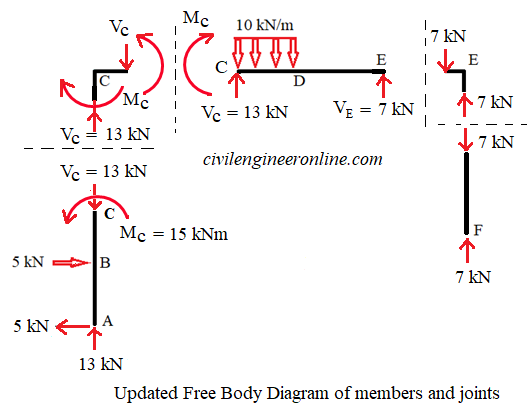
Figure 5-6(d)

Now we will draw Shear Force Diagram (SFD), Bending Moment Diagram (BMD) and Axial Force Diagram (AFD) of each member separately. We advise you to see our solved example Problem 5-2 for more knowledge about SFD and BMD of beam.

Shear force diagram, Bending Moment diagram and Axial Force diagram:

For member AB, we will consider the origin at A. All the forces acting perpendicular to the member will cotribute to shear force and bending moments while the forces along the length of the member will contribute to axial force. Compressive axial force is taken as negative and tensile is taken as positive.

SFD, BMD and AFD for member ABC are shown in Figure 5-6(e)

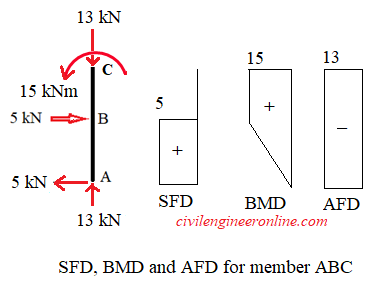
Figure 5-6(e)

For member CDE, we will consider the origin at C. We notice that there is no axial force in the member CDE. SFD and BMD is drawn by using the sign conventions as explained in Problem 5-2

SFD for CDE shows that there is a point of zero S.F. between C and D this means maximum bending moment will occur at this point. We can calculate this point by considering similarity of triangles in the SFD as follows;

13/5 = x / (2 - x); which gives x = 1.44 m. Therefore maximum B.M. will be at a distance of 1.44 m from C and equal to

M_max = 15 + 13 x 1.44 - 10 x 1.442/2 = 23.352 kNm

BMD will be parabolic under the uniform load. The SFD and BMD for CDE are shown in Figure 5-6(f)

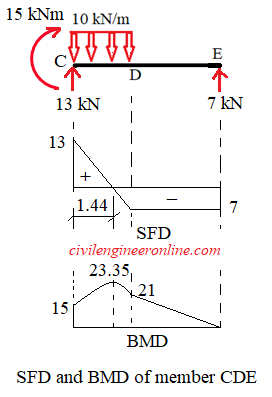
Figure 5-6(f)

For member EF, we consider the origin at E. The free body diagram of EF shows that member EF is subjected to only the axial force therefore there will be no shear force and bending moment in EF. The axial force diagram (AFD) for EF is shown in Figure 5-6(g)

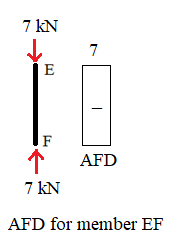
Figure 5-6(g)