Shear Force and Bending Moment Calculations and diagrams for double overhanging beam

Problem 5-5

Determine the values and draw the diagrams for shear force and bending moment due to the imposed load on overhanging beam shown in figure 5-5(a) and find the position of point of contra-flexure, if any.

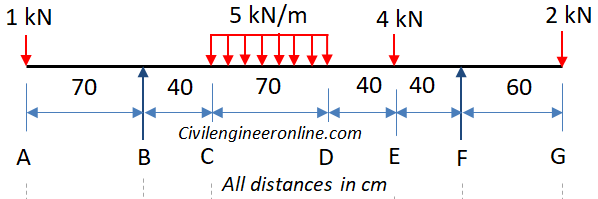
Figure 5-5(a)

Solution:

The given beam has two supports B and F and there are overhanging portions BA and FG on the left and right side respectively. For all the calculations we consider the origin of axes at point A and x-axis is considered positive in the right hand direction whereas y-axis is positive upwards.

This beam is statically determinate as there are only two vertical reactions at the supports, one each at  B and F and two equations of equilibrium (∑F_y = 0,  ∑M = 0) are available to solve for these reactions.

Now we apply the equations of equilibrium. Let the vertical reactions be  V_B at B and V_F at F.

Algebraic sum of all the forces equal to zero; ∑F_y = 0.

V_B + V_F – 1 – 5x0.7 – 4 – 2 = 0;

So,  V_B + V_F = 10.5 kN;      ………Eqn 1

Algebraic sum of the moments of all the forces about B = 0; ∑M = 0 about point B. For the moments of force we consider clockwise moments as negative and anti-clockwise moments as positive.

1 x0.7  - 5x0.7x(0.4+0.35) – 4 x(0.4+0.7+0.4) + V_F x (0.4+0.7+0.4+0.4) – 2x (0.4+0.7+0.4+0.4+0.6)=0;

On simplification we get; V_F x 1.9 = - 0.7 + 5x0.7x0.75 + 4x1.5 + 2x2.5;

1.9 V_F = 12.925;    ……. Eqn 2

Therefore V_F = 12.925/1.9;

We get V_F = 6.8 kN

Substituting the value of V_F in Eqn 1 we get;

V_B = 10.5 – 6.8 = 3.7 kN;

Shear Force Calculations

Sign Convention for Shear Force (SF):

1. If a force is trying to lift up the left hand side of a section the SF due to that force is taken as positive whereas a force trying to push the left hand side down is taken as negative.
2. In case a force lifts the right hand side of a section upward it will be taken as negative and if it is pushing it down the SF will be taken as positive.

In calculating SF we will move along the beam span from left to right (starting from origin at A)

The point A has a concentrated force of 1 kN acting downwards. In such cases we should calculate SF before and after the point. At a section just before A the SF will be zero because there is no force before point A. When we consider a section just after A the shear force will be -1 kN because there is a force of 1 kN at A trying to push the left hand side of the section downwards. We will follow the same procedure to calculate the shear force at all the main points of the beam (A, B, C, D, E, F, G). We get the following values.

SF Just before A = 0

SF just after A = -1 kN

SF just before B = - 1 kN (Note that V_B is not considered as it is acting exactly at A, not before A.

SF just after B = -1 + V_B = -1+ 3.7 = 2.7 kN   (Note that V_B is taken positive as it is acting upward)

SF just before C = -1 + V_B = -1+3.7 = 2.7 kN   (Note that there is no additional load between B and C hence SF at C is same as SF at B)

SF just after C = SF just before C = 2.7 kN (Note that in case of uniform load the SF will be same just before and after the section).

SF at D = -1 + V_B – 5x0.7 = -1+3.7 – 3.5 = - 0.8 kN

SF just before E = SF at D = - 0.8 kN

SF just after E = -1 + V_B – 5x0.7 – 4 = - 4.8 kN

SF just before F = -1 + V_B – 5x0.7 – 4 = - 4.8 kN (Note that there is no additional force between E and F)

SF just after F = -1 + V_B – 5x70 – 4 + 6.8 = 2 kN

SF just before G = SF just after F = 2 kN

SF just after G = SF just before G – 2 kN = 0   (2 kN load is acting exactly at G, therefore it will be considered when we calculate SF at a point after G. The shear force diagram (SFD) is shown in Fig 5.5(b)

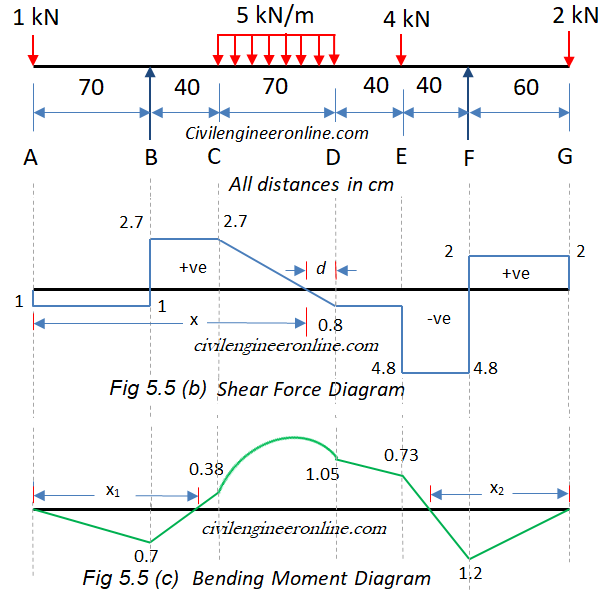
Figure 5-5(b) and (c)

Bending Moment Calculations

Sign convention for Bending Moment (BM):

1. The moments which try to bend the beam in such a way that it is concave downwards are known as sagging moments and are taken as positive.
2. The moments which try to bend the beam in such a way that it is convex upwards are known as hogging moments and are taken as negative.

As per the definition, bending moment at a section is the moment of resistance of the section. Numerically it is equal to the algebraic sum of moment of all the forces on either side of the section. In this example we will consider forces on the left hand side of the section and take the moment of those forces about the section.

BM at A = 1 x 0 = 0

BM at B = - 1 kN x 0.7 m = - 0.7 kNm       

BM at C = -1 x 1.1 + 3.7 x 0.4 = 0.38

BM at D = -1 x 1.8 + 3.7 x 1.1 – 5 x 0.7 x 0.35 = 1.05 kNm

BM at E = -1 x 2.2 + 3.7 x 1.5 – 5 x 0.7 x (0.35+0.4) =0.73 kNm

BM at F = -1 x 2.6 + 3.7 x 1.9 – 5 x 0.7 x (0.35+0.4+0.4) – 4 x 0.4 = -1.2 kNm

BM at G = -1 x 3.2 + 3.7 x 2.5 – 5 x 0.7 x (0.35+0.4+0.4+0.6) – 4 x 1.0 + 6.8 x 0.6 = 0

The bending moment diagram is shown in Fig. 5.5 (c) above.

Maximum Bending Moment will occur at the point where SF is zero.

From SFD it is clear that the SF will be zero somewhere between C and D.

We can determine the point of zero SF by two ways

 

Points of Contra-flexure

From the BMD we can see that there are two points at which the value of BM is zero and have opposite nature of bending on the two sides of these points; such points are known as points of contra-flexure.

One such point is between B and C and the other between E and F.

We can locate these points in an easy way by writing the equation of bending moment for that part of the beam and putting that value equal to zero.