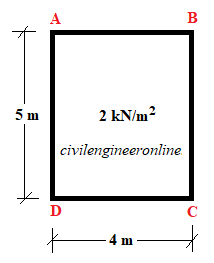
Figure 1-2(a)

Solution:

Fist we will check whether this slab panel ABCD is transferring the load in one way or two way. The ratio Long Side/Short Side = 5 / 4 = 1.25 less than 2

The ratio of long side to short side is less than 2 therefore the load distribution will be two-way, which means the load from slab will be transferred to supporting beam in two directions i.e. long direction and short direction. There are two beam AD and BC in the long direction and two beam AB and CD in the short direction.

In the case of two way slab panel we divide the area by dividing the 90 degree angles at each corner into two equal halves of 45 degree each. Let these angle bisectors meet at P and Q as given below

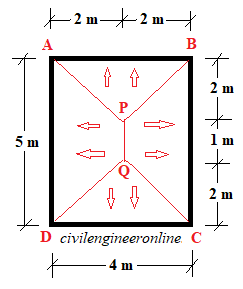
Figure 1-2(b)

Now the whole area is divided into four parts; two triangles and two trapeziums. Area of triangle ABP is connected to beam AB so it will transfer the load to beam AB. Similarly other areas will transfer the load to the connected beam. Triangle DQC will transfer the load to beam DC and trapezium BPQC will transfer the load to beam BC and trapezium APQD will transfer the load to beam AD.

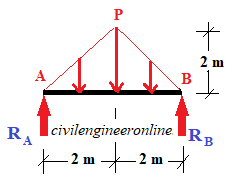
Figure 1-2(c)

The load on beam AB = load from area of ABP = area of triangle ABP x rate of floor load

Area of triangle ABP = 0.5 x base of triangle ABP x height of triangle ABP = 0.5 x 4 x 2 = 4 m²

Therefore the load transferred to beam AB = 4 m² x 2 kN/m² = 8 kN

As this load is in the form of a triangle its intensity will be maximum at the centre and it will be calculated as;

0.5 x 4 x w = 8 kN

Therefore w = 8/2 = 4 kNm

The reactions at A and B will equal to 8/2 =4 kN

Similarly we can calculate the load transferred by trapezoidal area BPQC to the connected beam BC.

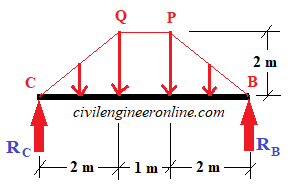
Figure 1-2(d)

Load on beam BC = Load from area BPQC = area of trapezium BPQC x rate of floor load

Area of trapezium BPQC = 0.5 x (sum of parallel sides) x height of trapezium

= 0.5 x (PQ + BC) x 2 = 0.5 x (1+ 5) x 2 = 6 m²

Therefore Load on BC = 6 m² x 2 kN/m² = 12 kN

As this load is trapezoidal in shape its maximum intensity w will be at P and Q which will be calculated in a simple way as;

0.5 x (1+5) x w = 12 kN

Therefore w = 12 / 3 = 4 kN/m

And the reactions at B and C will be equal to 12/2 = 6 kN

Now we find that at point B there are two reactions one from beam AB and the other from beam BC.

Therefore the total reaction at B = 4 + 6 = 10 kN

Sometimes its is required to represent the these triangular and trapezoidal loads in the form of a uniformly distributed Load (UDL).

We can transform the triangular load equivalent to uniformly distributed load (UDL) by using the following formula.

Equivalent Intensity of UDL = floor load intensity x short side/3

= (w) x (B)/3

= 2 x 4/3 = 2.667 kN/m

Similarly the trapezoidal load can also be transformed to equivalent UDL by using the following formula.

The equivalent UDL intensity of trapezoidal load = (w) x (B) x (3 - 1/(L/B)²) / 6

B= short side, L = long side, w = rate of floor load

Equivalent UDL intensity = 2 x 4 x (3 - 1/(5/4)²)/6

= 2 x 4 x (3 - 1/(1.25)²)/6 = 2 x 4 x 2.36/6 = 3.146 kN/m

You can also use our online calculator for tributory load from one way and two way slabs

Example 5-2 SFD and BMD for Simple beam

Example 5-3 SFD and BMD for Overhanging beam