Problem 7-2
A continuous beam with simple supports at A, B and C is subjected to the loading as shown in figure 7-2(a). Find the support reactions and draw Bending moment diagram.
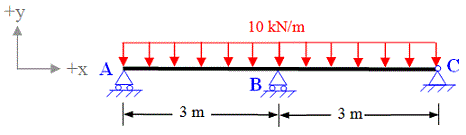
Figure 7-2(a)
Solution:
The free body diagram of this structure in figure 7-2(b) shows that the given beam has 4 support reactions (Cx ,Ay, By, Cy) whereas there are only 3 equations of equilibrium (ΣFx = 0; ΣFy = 0; and ΣMz = 0) available for this structure. Therefore it is statically indeterminate of degree one.
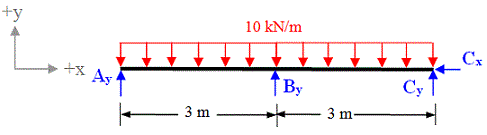
Figure 7-2(b)
To solve for the unknown reactions of this structure we need one more equation which can be obtained by compatibility. It is evident that deflection at all the supports is zero. Considering By as redundant R and applying principle of superposition we get;
Total deflection at B is equal to the sum of deflection due to applied loading and deflection due to redundant R (refer to figure 7-2(c).
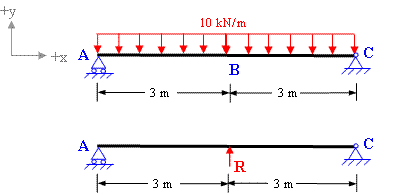
Figure 7-2(c)
Deflection at B due to applied loading
δLoad = 5 w L4 /384 EI ↓
δLoad = 5 x 10 x 64 /384 EI ↓
Deflection at B due to Redundant R
δR = R L3 /48 EI ↑
δR = R x 63 /48 EI ↑
Taking downward deflection as negative and upward as positive and applying principle of superposition.
ΣδB = R x 63 /48 EI - 5 x 10 x 64 /384 EI
But ΣδB = 0 as the support A is a rigid support.
Therefore
R x 63 /48 EI - 5 x 10 x 64 /384 EI =0
Hence R = 37.5 kN
Now we can easily determine the other reactions by applying the equations of static equilibrium;
ΣFy = 0;
Ay + 37.5 + Cy - 10 X 6 = 0;
Ay + Cy = 22.5
ΣMz = 0 (consider z-axis passing through A)
37.5 x 3 + 6 x Cy - 10 x 6 x 3 = 0;
Therefore Cy = 11.25 kN
and we get Ay = 22.5 - 11.25
Ay = 11.25 kN
The bending moment diagram is shown in figure 7-2(d)
The resultant BMD is drawn by superposing the diagrams of UDL and point load. It also shows the maximum Bending moment is greatly reduced which is = -56.25 +45 = -11.25 kNm. The BMD also shows that this beam will have two points of contra-flexure which can be determined in a simple way by writing the equation of bending moment at a distance x from A.
Mx = 11.25 x -10x2 /2 = 0 (from A to B)
Therefore x = 2.25m from the support A, and similarly another point of contra-flexure is at a distance of 2.25m from C,
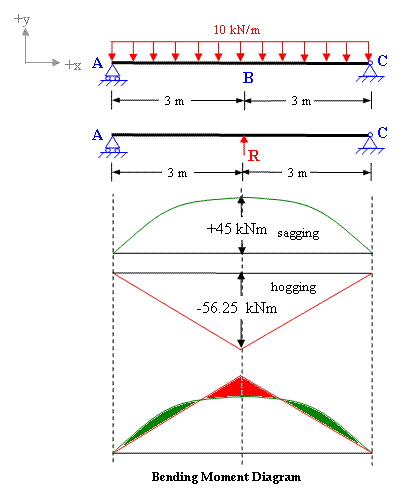
Fig 7-2(d)
You can also use our deflection calculator for finding the deflection to solve this problem
Please visit the following links of solved examples for Indeterminate Structures
You can also visit other solved examples
Excellent Calculators
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
More Links
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Contining Tall building worldwide
Forthcoming conferences
Contining List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
Search our website for more...
PleaseTell your Friends about us if you find our website useful
Other Useful Links
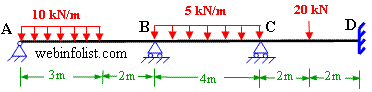 Problem
8-1New
Solution of Indeterminate beam by moment distribution method
Problem
8-1New
Solution of Indeterminate beam by moment distribution method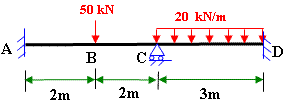 Problem 7-4 Solution of Indeterminate Structure by
slope-deflection equations
Problem 7-4 Solution of Indeterminate Structure by
slope-deflection equations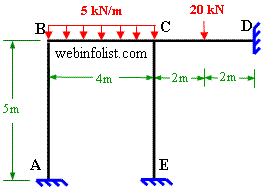 Problem 8-2 Solution of Indeterminate Frame by using moment distribution method
Problem 8-2 Solution of Indeterminate Frame by using moment distribution method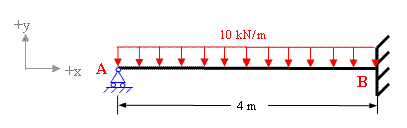 Problem 7-1 Solution of Indeterminate Structure by consistent deformation
Problem 7-1 Solution of Indeterminate Structure by consistent deformation