Problem 6-2
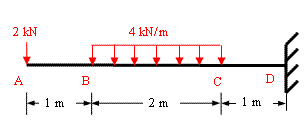
Use Macaulay's method to determine the values of slope and deflection at 5m from the left support due to imposed load as shown in figure 6-2(a). The material of beam has modulus of elasticity as 200 GPa. The beam cross-section is I-shaped with top and bottom flange width as 250 mm and thickness 20 mm, web height as 300 mm and web thickness as 15 mm.
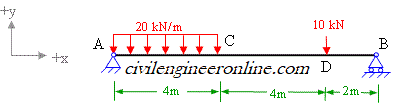
Figure 6-2(a)
Solution:
The loading is not same throughout the span, therefore we use Macaulay's Method for finding slope and deflection of the given beam.The given beam has two unknown reaction components which are calculated in Prob 4-1 as Ay = 66 kN and By = 24 kN;
The equivalent loading is shown in
figure 6-2(b).
Figure
6-2(b)
The differential equation of elastic curve for
this beam can be written as follows;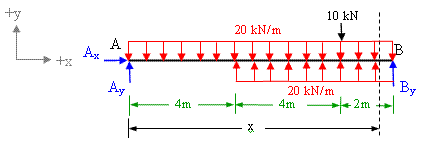
EI (d2y/dx2) = 66[x] - 20[x]2 /2 +20[x-4]2/2 - 10[x-8] Eq. 1
Integrating Eq. 1 we get;
EI(dy/dx) = 66[x]2/2 - 20[x]3 /6 +20[x-4]3/6 - 10[x-8]2/2 +C1 Eq.2
We do not have any information about slope at the ends,
We continue integrating Eq. 2 for finding deflection;
EIy = 66[x]3/6 - 20[x]4 /24 +20[x-4]4/24 - 10[x-8]3/6 +C1x + C2
Now apply the condition for deflection at the supports;
at x=0, y=0 (neglect the terms which become negative with x=0)
we get C2=0;
Further at x=10, y=0; we get
0=11000 - 200000/24 + 1080 - 80/6 + 10C1
C1= -374.66
Therefore the equation for slope can be written as
EI(dy/dx) = 66[x]2/2 - 20[x]3 /6 +20[x-4]3/6 - 10[x-8]2/2 - 374.66
and the equation for deflection would be
EIy = 66[x]3/6 - 20[x]4 /24 +20[x-4]4/24 - 10[x-8]3/6 - 374.66x
Slope at x=5;
dy/dx = (37)/EI
Deflection at x=5;
y = (- 1018)/EI
The value of moment of inertia can be calculated by using moment of inertia calculator
Ixx = 29008.3 cm4
EI= (200x109 N/m2)x(29008.3 cm4 ) = 58016.6 kN m2
substituting the value of EI in the expressions for slope and deflection we get;
dy/dx = 37/58016.6 = 0.00064 rad.
y = - 1018/58016.6 = - 0.0175 m (negative sign indicates that the deflection is downward)
You can also use our Slope deflection calculator for different combinations of load on Simple beam.
You can also visit the following related links of solved examples
Excellent Calculators
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
More Links
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall buildings worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
Search our website for more...
PleaseTell your Friends about us if you find our website useful
Other Useful Links