Moment Capacity of Reinforced Concrete beam
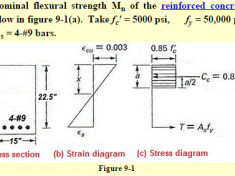
Calculation of nominal moment capacity of a singly reinforced concrete beam of rectangular section using Strength Design method as adopted by American Concrete Institute. This […]

Calculation of nominal moment capacity of a singly reinforced concrete beam of rectangular section using Strength Design method as adopted by American Concrete Institute. This […]
Copyright © 2025 | WordPress Theme by MH Themes