Maximum and Minimum Principal Stress Calculator
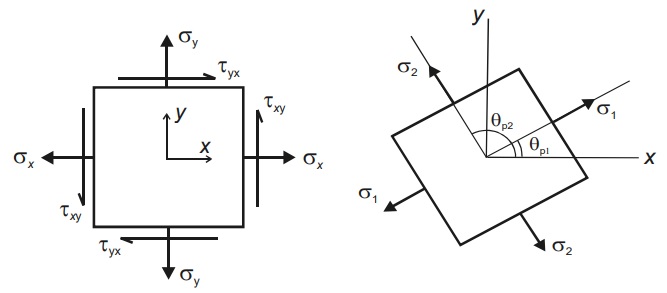
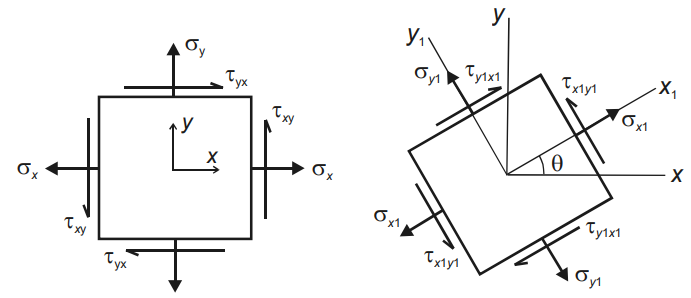
This calculator is for finding maximum and minimum in-plane principal stressess(σp1 and σp2) and the angle of orientation (θp1 and θp2) of the principal planes.
Sign Convention: If the outward normal to a plane is acting in the positive direction it is termed as positive face otherwise it is negative face. Normal stresses acting in the positive direction on the positive face or in the negative direction on a negative face are taken as positive whereas the normal stresses acting in the negative direction on a positive face or in the positive direction on a negative face are taken as negative. Shear stress is taken as positive if it acts in the positive coordinate direction on a positive face, or it acts in negative coordinate direction on negative face. Otherwise it is negative. Angle of orientation (θ) is -ve for clock-wise and +ve for anti-clockwise rotation with reference to the positive x-axis.
The angles of principal planes are at right angles to each other.
By default this calculator is using the units of stress as MPa, but other units N/mm2, kN/m2, ksi, psi etc. can also be used without affecting the results.
This calculator can also be used for principal strains because the equations are same in that case also, just by ignoring the units as strains are dimensionless.
Please refer to the figure and enter the required values in the form given below and then click "Calculate".
The following Principal Stress Equations are used in this calculator
You are also welcome to send your Feedback
Please Tell your Friends about us
Keep visiting for getting updated or Join our mailing list to get updates
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Shear Stress Calculator
Calculate Transverse Shear Stress for beam sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the Strength of Reinforced Concrete beam
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for bending moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Statically Indeterminate Structures
Definition and methods of solving
Truss Member Forces calculation
using method of joints and method of sections
Shear force and bending moment
Illustrated solved examples to draw shear force and bending moment diagrams
Slope and deflection of beam and Truss
Illustrated solved examples to determine slope and deflection of beam and truss
Solution of indeterminate structures
slope deflection, moment distribution etc.
Reinforced concrete beam
Solved examples to determine the strength and other parameters
Calculation of bending stress in a beam
using bending equation and plotting the bending stress diagram
Skyscrapers of the world
Containing Tall building worldwide
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Please Tell your Friends about us
