Problem 5-5
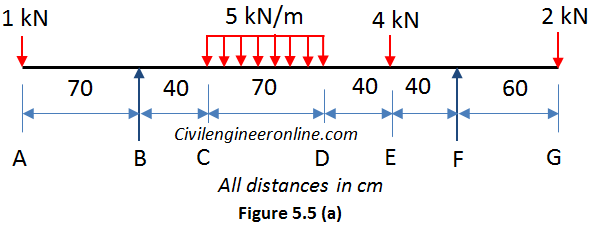
Draw the Shear force and bending moment diagrams for the overhanging beam given in figure 5.5(a) above. Also determine maximum bending moment and the points of contra-flexure.
Click here to Get complete solution of this problem
[fblike]
Solving for SFD and BMD of Overhanging beam: Prob 5.5
Leave a Reply
You must be logged in to post a comment.